Exercise 2.1 Page: 28
1. The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Solutions:
Graphical method to find zeroes:-
Total number of zeroes in any polynomial equation = total number of times the curve intersects x-axis.
(i) In the given graph, the number of zeroes of p(x) is 0 because the graph is parallel to x-axis does not cut it at any point.
(ii) In the given graph, the number of zeroes of p(x) is 1 because the graph intersects the x-axis at only one point.
(iii) In the given graph, the number of zeroes of p(x) is 3 because the graph intersects the x-axis at any three points.
(iv) In the given graph, the number of zeroes of p(x) is 2 because the graph intersects the x-axis at two points.
(v) In the given graph, the number of zeroes of p(x) is 4 because the graph intersects the x-axis at four points.
(vi) In the given graph, the number of zeroes of p(x) is 3 because the graph intersects the x-axis at three points.
Exercise 2.2 Page: 33
1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
Solutions:
(i) x2–2x –8
⇒x2– 4x+2x–8 = x(x–4)+2(x–4) = (x-4)(x+2)
Therefore, zeroes of polynomial equation x2–2x–8 are (4, -2)
Sum of zeroes = 4–2 = 2 = -(-2)/1 = -(Coefficient of x)/(Coefficient of x2)
Product of zeroes = 4×(-2) = -8 =-(8)/1 = (Constant term)/(Coefficient of x2)
(ii) 4s2–4s+1
⇒4s2–2s–2s+1 = 2s(2s–1)–1(2s-1) = (2s–1)(2s–1)
Therefore, zeroes of polynomial equation 4s2–4s+1 are (1/2, 1/2)
Sum of zeroes = (½)+(1/2) = 1 = -(-4)/4 = -(Coefficient of s)/(Coefficient of s2)
Product of zeros = (1/2)×(1/2) = 1/4 = (Constant term)/(Coefficient of s2 )
(iii) 6x2–3–7x
⇒6x2–7x–3 = 6x2 – 9x + 2x – 3 = 3x(2x – 3) +1(2x – 3) = (3x+1)(2x-3)
Therefore, zeroes of polynomial equation 6x2–3–7x are (-1/3, 3/2)
Sum of zeroes = -(1/3)+(3/2) = (7/6) = -(Coefficient of x)/(Coefficient of x2)
Product of zeroes = -(1/3)×(3/2) = -(3/6) = (Constant term) /(Coefficient of x2 )
(iv) 4u2+8u
⇒ 4u(u+2)
Therefore, zeroes of polynomial equation 4u2 + 8u are (0, -2).
Sum of zeroes = 0+(-2) = -2 = -(8/4) = = -(Coefficient of u)/(Coefficient of u2)
Product of zeroes = 0×-2 = 0 = 0/4 = (Constant term)/(Coefficient of u2 )
(v) t2–15
⇒ t2 = 15 or t = ±√15
Therefore, zeroes of polynomial equation t2 –15 are (√15, -√15)
Sum of zeroes =√15+(-√15) = 0= -(0/1)= -(Coefficient of t) / (Coefficient of t2)
Product of zeroes = √15×(-√15) = -15 = -15/1 = (Constant term) / (Coefficient of t2 )
(vi) 3x2–x–4
⇒ 3x2–4x+3x–4 = x(3x-4)+1(3x-4) = (3x – 4)(x + 1)
Therefore, zeroes of polynomial equation3x2 – x – 4 are (4/3, -1)
Sum of zeroes = (4/3)+(-1) = (1/3)= -(-1/3) = -(Coefficient of x) / (Coefficient of x2)
Product of zeroes=(4/3)×(-1) = (-4/3) = (Constant term) /(Coefficient of x2 )
2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) 1/4 , -1
Solution:
From the formulas of sum and product of zeroes, we know,
Sum of zeroes = α+β
Product of zeroes = α β
Sum of zeroes = α+β = 1/4
Product of zeroes = α β = -1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2–(1/4)x +(-1) = 0
4x2–x-4 = 0
Thus,4x2–x–4 is the quadratic polynomial.
(ii)√2, 1/3
Solution:
Sum of zeroes = α + β =√2
Product of zeroes = α β = 1/3
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2 –(√2)x + (1/3) = 0
3x2-3√2x+1 = 0
Thus, 3x2-3√2x+1 is the quadratic polynomial.
(iii) 0, √5
Solution:
Given,
Sum of zeroes = α+β = 0
Product of zeroes = α β = √5
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly
as:-
x2–(α+β)x +αβ = 0
x2–(0)x +√5= 0
Thus, x2+√5 is the quadratic polynomial.
(iv) 1, 1
Solution:
Given,
Sum of zeroes = α+β = 1
Product of zeroes = α β = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2–x+1 = 0
Thus , x2–x+1is the quadratic polynomial.
(v) -1/4, 1/4
Solution:
Given,
Sum of zeroes = α+β = -1/4
Product of zeroes = α β = 1/4
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2–(-1/4)x +(1/4) = 0
4x2+x+1 = 0
Thus,4x2+x+1 is the quadratic polynomial.
(vi) 4, 1
Solution:
Given,
Sum of zeroes = α+β =4
Product of zeroes = αβ = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x+αβ = 0
x2–4x+1 = 0
Thus, x2–4x+1 is the quadratic polynomial.
Exercise 2.3 Page: 36
1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3-3x2+5x–3 , g(x) = x2–2
Solution:
Given,
Dividend = p(x) = x3-3x2+5x–3
Divisor = g(x) = x2– 2

Therefore, upon division we get,
Quotient = x–3
Remainder = 7x–9
(ii) p(x) = x4-3x2+4x+5 , g(x) = x2+1-x
Solution:
Given,
Dividend = p(x) = x4 – 3x2 + 4x +5
Divisor = g(x) = x2 +1-x

Therefore, upon division we get,
Quotient = x2 + x–3
Remainder = 8
(iii) p(x) =x4–5x+6, g(x) = 2–x2
Solution:
Given,
Dividend = p(x) =x4 – 5x + 6 = x4 +0x2–5x+6
Divisor = g(x) = 2–x2 = –x2+2
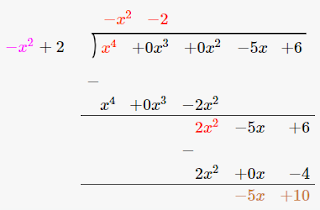
Therefore, upon division we get,
Quotient = -x2-2
Remainder = -5x + 10
2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t2-3, 2t4 +3t3-2t2-9t-12
Solutions:
Given,
First polynomial = t2-3
Second polynomial = 2t4 +3t3-2t2 -9t-12

As we can see, the remainder is left as 0. Therefore, we say that, t2-3 is a factor of 2t4 +3t3-2t2 -9t-12.
(ii)x2+3x+1 , 3x4+5x3-7x2+2x+2
Solutions:
Given,
First polynomial = x2+3x+1
Second polynomial = 3x4+5x3-7x2+2x+2

As we can see, the remainder is left as 0. Therefore, we say that, x2 + 3x + 1 is a factor of 3x4+5x3-7x2+2x+2.
(iii) x3-3x+1, x5-4x3+x2+3x+1
Solutions:
Given,
First polynomial = x3-3x+1
Second polynomial = x5-4x3+x2+3x+1

As we can see, the remainder is not equal to 0. Therefore, we say that, x3-3x+1 is not a factor of x5-4x3+x2+3x+1 .
3. Obtain all other zeroes of 3x4+6x3-2x2-10x-5, if two of its zeroes are √(5/3) and – √(5/3).
Solutions:
Since this is a polynomial equation of degree 4, hence there will be total 4 roots.
√(5/3) and – √(5/3) are zeroes of polynomial f(x).
∴ (x –√(5/3)) (x+√(5/3) = x2-(5/3) = 0
(3x2−5)=0, is a factor of given polynomial f(x).
Now, when we will divide f(x) by (3x2−5) the quotient obtained will also be a factor of f(x) and the remainder will be 0.

Therefore, 3x4 +6x3 −2x2 −10x–5 = (3x2 –5)(x2+2x+1)
Now, on further factorizing (x2+2x+1) we get,
x2+2x+1 = x2+x+x+1 = 0
x(x+1)+1(x+1) = 0
(x+1)(x+1) = 0
So, its zeroes are given by: x= −1 and x = −1.
Therefore, all four zeroes of given polynomial equation are:
√(5/3),- √(5/3) , −1 and −1.
Hence, is the answer.
4. On dividing x3-3x2+x+2 by a polynomial g(x), the quotient and remainder were x–2 and –2x+4, respectively. Find g(x).
Solution:
Given,
Dividend, p(x) = x3-3x2+x+2
Quotient = x-2
Remainder = –2x+4
We have to find the value of Divisor, g(x) =?
As we know,
Dividend = Divisor × Quotient + Remainder
∴ x3-3x2+x+2 = g(x)×(x-2) + (-2x+4)
x3-3x2+x+2-(-2x+4) = g(x)×(x-2)
Therefore, g(x) × (x-2) = x3-3x2+3x-2
Now, for finding g(x) we will divide x3-3x2+3x-2 with (x-2)

Therefore, g(x) = (x2–x+1)
5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solutions:
According to the division algorithm, dividend p(x) and divisor g(x) are two polynomials, where g(x)≠0. Then we can find the value of quotient q(x) and remainder r(x), with the help of below given formula;
Dividend = Divisor × Quotient + Remainder
∴ p(x) = g(x)×q(x)+r(x)
Where r(x) = 0 or degree of r(x)< degree of g(x).
Now let us proof the three given cases as per division algorithm by taking examples for each.
(i) deg p(x) = deg q(x)
Degree of dividend is equal to degree of quotient, only when the divisor is a constant term.
Let us take an example, p(x) = 3x2+3x+3 is a polynomial to be divided by g(x) = 3.
So, (3x2+3x+3)/3 = x2+x+1 = q(x)
Thus, you can see, the degree of quotient q(x) = 2, which also equal to the degree of dividend p(x).
Hence, division algorithm is satisfied here.
(ii) deg q(x) = deg r(x)
Let us take an example, p(x) = x2 + 3 is a polynomial to be divided by g(x) = x – 1.
So, x2 + 3 = (x – 1)×(x) + (x + 3)
Hence, quotient q(x) = x
Also, remainder r(x) = x + 3
Thus, you can see, the degree of quotient q(x) = 1, which is also equal to the degree of remainder r(x).
Hence, division algorithm is satisfied here.
(iii) deg r(x) = 0
The degree of remainder is 0 only when the remainder left after division algorithm is constant.
Let us take an example, p(x) = x2 + 1 is a polynomial to be divided by g(x) = x.
So, x2 + 1 = (x)×(x) + 1
Hence, quotient q(x) = x
And, remainder r(x) = 1
Clearly, the degree of remainder here is 0.
Hence, division algorithm is satisfied here.
Exercise 2.4 Page: 36
1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3+x2-5x+2; -1/2, 1, -2
Solution:
Given, p(x) = 2x3+x2-5x+2
And zeroes for p(x) are = 1/2, 1, -2
∴ p(1/2) = 2(1/2)3+(1/2)2-5(1/2)+2 = (1/4)+(1/4)-(5/2)+2 = 0
p(1) = 2(1)3+(1)2-5(1)+2 = 0
p(-2) = 2(-2)3+(-2)2-5(-2)+2 = 0
Hence, proved 1/2, 1, -2 are the zeroes of 2x3+x2-5x+2.
Now, comparing the given polynomial with general expression, we get;
∴ ax3+bx2+cx+d = 2x3+x2-5x+2
a=2, b=1, c= -5 and d = 2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax3+bx2+cx+d , then;
α +β+γ = –b/a
αβ+βγ+γα = c/a
α βγ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α+β+γ = ½+1+(-2) = -1/2 = –b/a
αβ+βγ+γα = (1/2×1)+(1 ×-2)+(-2×1/2) = -5/2 = c/a
α β γ = ½×1×(-2) = -2/2 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.
(ii) x3-4x2+5x-2 ;2, 1, 1
Solution:
Given, p(x) = x3-4x2+5x-2
And zeroes for p(x) are 2,1,1.
∴ p(2)= 23-4(2)2+5(2)-2 = 0
p(1) = 13-(4×12 )+(5×1)-2 = 0
Hence proved, 2, 1, 1 are the zeroes of x3-4x2+5x-2
Now, comparing the given polynomial with general expression, we get;
∴ ax3+bx2+cx+d = x3-4x2+5x-2
a = 1, b = -4, c = 5 and d = -2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax3+bx2+cx+d , then;
α + β + γ = –b/a
αβ + βγ + γα = c/a
α β γ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α +β+γ = 2+1+1 = 4 = -(-4)/1 = –b/a
αβ+βγ+γα = 2×1+1×1+1×2 = 5 = 5/1= c/a
αβγ = 2×1×1 = 2 = -(-2)/1 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.
2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.
Solution:
Let us consider the cubic polynomial is ax3+bx2+cx+d and the values of the zeroes of the polynomials be α, β, γ.
As per the given question,
α+β+γ = -b/a = 2/1
αβ +βγ+γα = c/a = -7/1
α βγ = -d/a = -14/1
Thus, from above three expressions we get the values of coefficient of polynomial.
a = 1, b = -2, c = -7, d = 14
Hence, the cubic polynomial is x3-2x2-7x+14
3. If the zeroes of the polynomial x3-3x2+x+1 are a – b, a, a + b, find a and b.
Solution:
We are given with the polynomial here,
p(x) = x3-3x2+x+1
And zeroes are given as a – b, a, a + b
Now, comparing the given polynomial with general expression, we get;
∴px3+qx2+rx+s = x3-3x2+x+1
p = 1, q = -3, r = 1 and s = 1
Sum of zeroes = a – b + a + a + b
-q/p = 3a
Putting the values q and p.
-(-3)/1 = 3a
a=1
Thus, the zeroes are 1-b, 1, 1+b.
Now, product of zeroes = 1(1-b)(1+b)
-s/p = 1-b2
-1/1 = 1-b2
b2 = 1+1 = 2
b = ±√2
Hence,1-√2, 1 ,1+√2 are the zeroes of x3-3x2+x+1.
4. If two zeroes of the polynomial x4-6x3-26x2+138x-35 are 2 ±√3, find other zeroes.
Solution:
Since this is a polynomial equation of degree 4, hence there will be total 4 roots.
Let f(x) = x4-6x3-26x2+138x-35
Since 2 +√3 and 2-√3 are zeroes of given polynomial f(x).
∴ [x−(2+√3)] [x−(2-√3)] = 0
(x−2−√3)(x−2+√3) = 0
On multiplying the above equation we get,
x2-4x+1, this is a factor of a given polynomial f(x).
Now, if we will divide f(x) by g(x), the quotient will also be a factor of f(x) and the remainder will be 0.

So, x4-6x3-26x2+138x-35 = (x2-4x+1)(x2 –2x−35)
Now, on further factorizing (x2–2x−35) we get,
x2–(7−5)x −35 = x2– 7x+5x+35 = 0
x(x −7)+5(x−7) = 0
(x+5)(x−7) = 0
So, its zeroes are given by:
x= −5 and x = 7.
Therefore, all four zeroes of given polynomial equation are: 2+√3 , 2-√3, −5 and 7.
